統計学をビジネスに応用するには、個別の統計手法を学ぶだけではなく、それらを目的に応じて適切に選び、組み合わせる能力が重要です。
- 回帰モデル、時系列モデル、ベイズモデル、ディープラーニングモデルなどいっぱいありすぎてよくわからない
- 統計モデル同士のつながりや使い分けができない
本記事ではビジネス統計学の体系的な理解に向けて、各統計手法の特徴、連携方法、そして適切な使い分けについて詳細に解説します。
統計の基礎知識をお持ちの方が、より俯瞰的な視点で統計手法を捉えられるよう、実践的なアプローチを提示します。
統計学の学習における基本的な視点

統計学を体系的に学ぶためには、単一の手法を深堀りするのではなく、各モデルの関係性と適用領域を理解することが重要です。
目的、数理的基盤、実践的な活用の観点から統計モデルを俯瞰することで、より深い洞察が得られます。
現代のデータサイエンスにおいて、統計モデルは意思決定のための不可欠な要素となっています。
各モデルの特性を正確に理解し、適切に選択・活用することが、ビジネス戦略の成功につながります。
モデル選択は単なる技術的判断ではなく、ビジネス課題の本質を理解する思考プロセスです。
データの性質、目的、計算リソースなど、多角的な観点から最適なアプローチを見出すことが求められます。
統計手法の役割:目的別に整理する
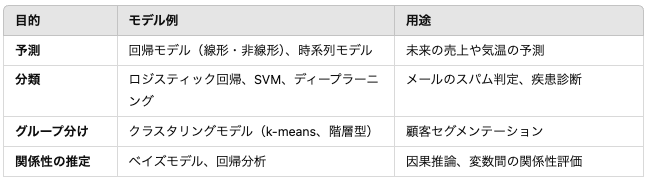
統計手法を体系的に理解するためには、まず目的別に整理することが重要です。
それぞれの手法が解決する課題や用途を明確にすることで、適切な手法を選ぶ基準が得られます。
予測:未来を見通すためのモデル
- 適用範囲:売上予測、需要予測など。
- 主な手法:線形回帰、時系列モデル(ARIMA、LSTM)。
- 特徴:過去のデータを用いて未来の値を推定。
回帰モデルや時系列モデルは、過去のデータから将来の傾向を予測するための強力な手法です。
線形回帰、非線形回帰、ARIMAモデルなど、各モデルの特性を理解し、適切なシナリオで活用することが重要です。
分類とクラスタリング:データの整理
- 適用範囲:スパムメール判定、顧客分類。
- 主な手法:ロジスティック回帰、SVM、k-meansクラスタリング。
- 特徴:ラベル付きデータ(分類)とラベルなしデータ(クラスタリング)に応じた手法を選択。
分類ではラベル付きデータの有無が鍵となり、クラスタリングは潜在的なグループを特定する際に有効です。
ロジスティック回帰、サポートベクターマシン(SVM)、ディープラーニングは、データを特定のカテゴリに分類するための高度な統計的手法です。
各モデルの特徴を理解し、ビジネス課題に応じて適切なモデルを選択することが求められます。
関係性の推定:変数間のつながりを探る
- 適用範囲:因果関係の推定、パフォーマンス評価。
- 主な手法:ベイズ推定、回帰分析。
- 特徴:データ間の因果関係や影響度を定量化。
関係性の推定は、施策の効果検証や戦略立案において欠かせない要素です。
統計モデルの基盤:数学的つながりを学ぶ

統計モデルは共通する数理的基盤を持つ場合が多く、これを理解することで手法間の連携が見えてきます。
線形回帰とロジスティック回帰の共通点
- 共通基盤:線形代数。
- 違い:連続値の出力(線形回帰)と確率の出力(ロジスティック回帰)。
数学的基盤を理解することで、異なる手法が補完的に使える状況を見極められます。
時系列モデルと回帰分析の関連性
- 共通基盤:データ予測。
- 違い:時系列データの時間依存性を考慮する点。
データの性質に応じて、時系列分析と回帰分析を切り替えることが重要です。
ディープラーニングとベイズ推定の相互補完
- 共通基盤:確率論。
- 違い:データ駆動型(ディープラーニング)と理論駆動型(ベイズ推定)。
これらの手法を使い分けることで、複雑な課題にも柔軟に対応できます。
選択の基準:データ特性とビジネス課題に基づく判断
統計手法の選択は、データの性質やビジネス課題に応じて変わります。具体的な選択基準を整理します。
データ量と計算リソース
- 少量データ(<100サンプル)
- 線形回帰
- 単純なロジスティック回帰
- ベイズモデル
- 特徴: パラメータ数が少ない、過学習リスク低い
- 中規模データ(100-10,000サンプル)
- サポートベクターマシン(SVM)
- 決定木
- ランダムフォレスト
- 特徴: 中程度の複雑さ、汎化性能良好
- 大規模データ(>10,000サンプル)
- ディープラーニング
- 勾配ブースティング
- ニューラルネットワーク
- 特徴: 高い特徴量抽出能力、複雑なパターン認識
データ規模と計算リソースに応じた手法選択が必要です。
変数の性質による分類
- 連続変数
- 線形回帰
- 重回帰分析
- 主成分分析(PCA)
- カテゴリカル変数
- ロジスティック回帰
- 決定木
- クラスタリング
- 混合変数
- ランダムフォレスト
- グラフィカルモデル
- ベイズネットワーク
変数は定義に従うだけであるが、実際に扱う変数とモデルで使用可能な変数がズレていてよくわからない結果になることはよくあります。
モデルの複雑性と解釈性
- 単純モデル
- 解釈が容易
- 計算コスト低い
- 例: 線形回帰、ロジスティック回帰
- 中程度の複雑さ
- バランスの取れたモデル
- 例: ランダムフォレスト、勾配ブースティング
- 高度に複雑なモデル
- 非線形性、高次元データ対応
- 例: ディープラーニング、ニューラルネットワーク
ビジネスでの説明責任を考慮し、解釈性が求められる場合にはシンプルなモデルを優先します。
実践フレームワーク:統計手法を効果的に活用する方法

理論的な知識を実際のビジネス課題に適用するためのフレームワークを紹介します。
データ分析やモデル選択において成功するためには、系統立ててプロセスを進めることが重要です。
データ理解
モデル選択の第一歩は、データの特性を正確に把握することです。
各変数の種類(数値型、カテゴリ型など)を確認し、欠損値や外れ値が存在する場合はその対処方法を検討します。
また、変数間の相関を評価することで、モデル構築に適した特徴量を見極めることが可能です。
データ量も重要で、サンプルサイズが不足している場合にはデータ拡張やブートストラップ法を用いることが考えられます。
さらに、時間的な特性を持つデータ(例: 時系列データ)では、季節性やトレンドの有無を確認し、データ収集の頻度が適切かを検討します。
このように、データ理解はモデル選択の成功に直結する重要なステップです。
モデル仮定の検証
次に、選択するモデルがデータに適合するかどうかを検証します。
線形回帰モデルやロジスティック回帰モデルのような一般的な統計モデルでは、独立変数と従属変数の間に線形関係が存在することが仮定されます。
この仮定を散布図や残差プロットで確認します。
また、データサンプル間の独立性も確認する必要があります。
特に時系列データの場合、自己相関がないかをチェックします。
さらに、データが正規分布に従う必要があるモデルの場合は、シャピロ・ウィルク検定やQ-Qプロットを使って正規性を検証します。
仮定が満たされない場合には、対数変換やBox-Cox変換などの前処理を施すことが有効です。
初期モデル構築
モデル構築は、シンプルなアプローチから段階的に進めるのが基本です。
最初は単純な線形モデルやロジスティック回帰のようなベースラインモデルを構築し、結果を確認します。
その後、階層モデルや非線形モデルなど、より複雑なモデルを試みることで、精度の向上を図ります。
特徴量選択も重要なプロセスです。
全ての変数を含めるのではなく、ステップワイズ法やLASSO回帰を活用し、重要な特徴量を選択します。
この手法により、モデルの解釈性と汎化性能が向上します。
4. モデル比較と選択
複数のモデルを構築した後は、パフォーマンスを比較して最適なものを選びます。
評価指標は、回帰モデルならR²やRMSE、分類モデルなら精度やF1スコア、ROC-AUC、時系列モデルはMAEやRMSEが役立ちます。
モデル選択では、過学習に注意が必要です。
K-foldクロスバリデーションを行うことで、モデルの汎化性能を評価します。
トレーニングデータとテストデータの性能差が大きい場合は、過学習が疑われるため、正則化やデータ量の増加を検討します。
5. 継続的な改善
一度モデルを選択した後も、継続的な改善を行うことが重要です。
定期的にモデルを再評価し、新しいデータを用いてその性能を確認します。
データが更新される場合や分析の目的が変化した場合には、特徴量やモデル構造を見直す必要があります。
また、モデルのパフォーマンスを定期的にモニタリングし、現実の状況に適応するように調整を行います。
これにより、モデルの信頼性と実用性を維持できます。
まとめ
統計学の本質は、データから意味を引き出し、ビジネス上の意思決定を支援することです。
各モデルの特性を理解し、目的に応じて適切に選択・活用することが、データサイエンスの真の力となります。
継続的な学習と実践を通じて、統計モデルをビジネス戦略の強力な武器へと昇華させていくことが重要です。



コメント