強化学習とは、機械学習の深層学習の中で、「教師あり学習」と「教師なし学習」と並立する概念です。
教師あり学習は、統計学の予測モデルとして解釈できますし、教師なし学習は統計学の分類モデルの半自動化として解釈できます。
これに対して、強化学習とはどんな概念なのでしょうか。
確率統計的でありながら、ゲーム理論的な要素も多く含む面白さを解説します。
1. 強化学習と確率統計
強化学習は、確率モデルの基礎を持ち、特に**マルコフ決定過程(MDP)**の枠組みで定義されています。
確率統計的な要素は以下の通りです:
確率的な側面
- 状態遷移確率:
- エージェントが行動を取ったとき、次の状態が確率的に決定される。
- 状態遷移モデル P(s′∣s,a)は、ある状態 s で行動 a を取ったときの次の状態 s′ の確率分布を表す。
- 期待値:
- 将来の累積報酬 Gt を期待値で評価し、最適な行動を選ぶ。
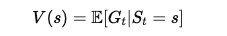
統計的推論
強化学習では、環境の完全なモデルが分からない場合に、試行錯誤を通じて報酬や遷移確率を推定します。
- 例: モンテカルロ法、時間差分学習(TD Learning)。
これらは確率統計の理論に深く依存しています。
確率統計的な枠組みの結論
強化学習は確率統計に基づき、環境の不確実性や将来の報酬の期待値を考慮して行動を最適化します。
- 例: Q学習やSARSAは、確率モデルを使った数値最適化アルゴリズムです。
2. 強化学習とゲーム理論
強化学習は、特に多エージェント環境や競争的状況では、ゲーム理論に非常に近い性質を持ちます。
ゲーム理論的な側面
- 多エージェント環境:
- 複数のエージェントが存在する場合、それぞれのエージェントが他のエージェントの行動を考慮して最適化する必要があります。
- これは、ゲーム理論におけるナッシュ均衡(Nash Equilibrium)の考え方に似ています。
- 戦略的行動:
- エージェントは、他のエージェントの行動に対して最善の反応(Best Response)を学習します。
- 例: ゲームAI(チェスや将棋)での戦略学習。
ゼロサムゲームと協力ゲーム
強化学習は、ゼロサムゲーム(一方の勝利が他方の損失)や協力ゲーム(複数のエージェントが報酬を共有する)にも適用可能です。
- 例: AlphaGoの対戦モデルはゼロサムゲームの理論に基づいています。
- 複数のロボットが協力してタスクを達成する場合、協力ゲームとして学習が行われます。
ゲーム理論的枠組みの結論
強化学習は、多エージェント環境ではゲーム理論的な行動戦略の学習に近づく。
*エージェントとは、強化学習のプログラム自体で、人間は環境に組み込まれるエージェントに含まれない。
- 例: マルチエージェント強化学習(Multi-Agent Reinforcement Learning, MARL)。
3. 確率統計とゲーム理論の融合
強化学習は、確率統計とゲーム理論を組み合わせたような構造を持っています:
- 確率統計的側面:
- 単一エージェント環境における不確実性の処理と最適化。
- ゲーム理論的側面:
- 多エージェント環境における他者の行動を考慮した戦略学習。
これを示す例として、**自己プレイ(Self-Play)**があります:
- 強化学習エージェントが自分自身と対戦しながら戦略を学習するプロセス。
- AlphaGoなどのモデルでは、自己プレイを通じてナッシュ均衡に近い戦略を学習。
4. 強化学習はどちらに近いのか?

単一エージェント環境では確率統計に近い
確率モデルに基づいて、環境内の最適化問題を解決する。
多エージェント環境ではゲーム理論に近い
他のエージェントの行動を考慮しながら学習するため、戦略的な行動選択が中心となる。
5. 結論
強化学習は、単一エージェント環境では確率統計に近く、多エージェント環境や競争的状況ではゲーム理論に近い性質を持つ分野です。
したがって、問題設定や環境の構造によって、どちらに近いかが変わります。
両方の要素を融合した強化学習の応用が、現在の最先端技術(ゲームAI、自律ロボットなど)を支えています。



コメント